关于计算机操作系统的一些思考

OS

• 最近正好在复习计算机系基础，这里就总结一些一些东西，同时记下我自己关于计算机系统学习的一点思考和体会，当然这个也是对CSAPP的再次回顾。
• 发现一个奇巧的东西，先按ctrl然后按tab可以实现整个段的tab

补码横空出世

• 简化了底层电路运算的设计，加减统一了，实现运算器的时候只需要根据加还是减法的标记位进行减数的取反。
• 注意，对于无符号数和有符号数，他们的最大位为1其他位全0的数互为相反数。这种特殊情况值得注意一下。
• 如果同时存在有符号数和无符号数，一个表达式里，会讲有符号提升为无符号，至于编译器确定字面值时，根据范围去确定有无符号，有点奇巧。但是最新标准中是符合直觉的
• 浮点数的设计很巧妙，具体记住几个关键点就可以了。尾数省略了一个1，阶数一个bias，等于2^(k-1) -1k=8/12两种精度下的取值，同时全0和最大是非规格数 ，阶码为0 用于表示0。 以及首位为0的数保证一个平滑地过渡。阶码最大就是NaN 和无穷大的表示。同时 符号位决定这个异常是否通知。1通知 符号位1是负数，注意小数部分的转换成二进制的方法。乘基取余，然后顺序从上至下。 总算知道为什么忽略1可以提高表示范围了，因为一个二进制数的第一位一定是1。 知道一个ascii 中数字刚好对应十六进制表示的30H 开始
• 注意按位运算 ~ 和逻辑运算 !
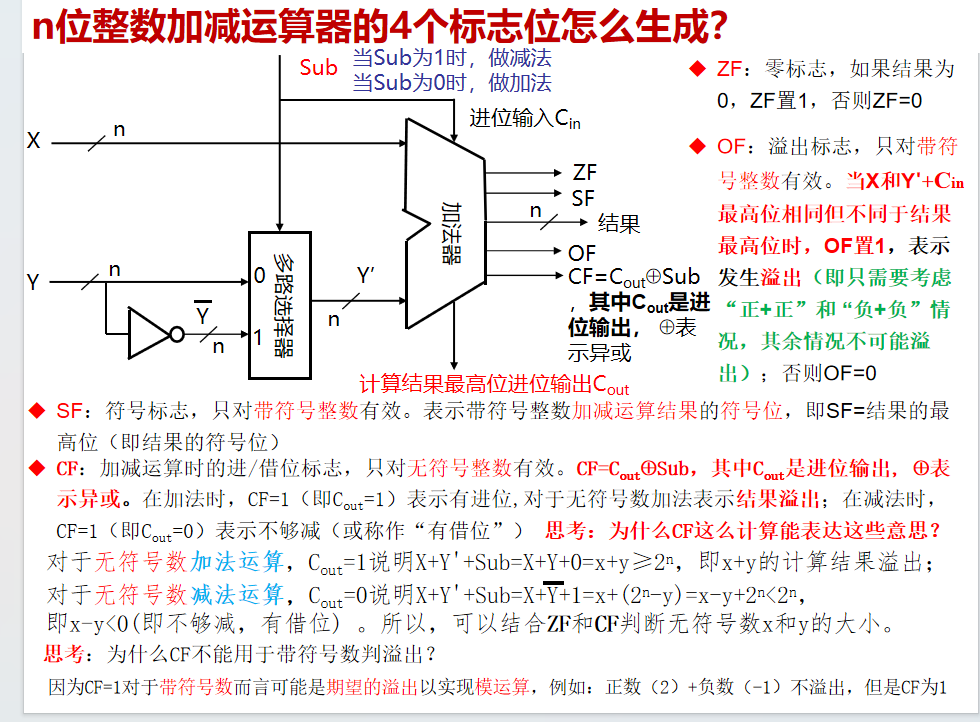
• 基于位运算的认识，以及补码，无符号有符号运算的认识，我们可以设计加法器，这个也正式引入一些控制信号，ZF CF OF SF。在汇编语言中我们也会再次见到 这四个标志位的设置非常简洁巧妙
• 
• 浮点运算 对阶，检查阶数是否正确。总结一下，布尔代数的完整性和数学上的正确性，保证了计算机数据运算的合理，我们只需要做的就是从工程上实现布尔代数。 这一部分可以作为了解，锻炼思考能力，不用强行记忆。

汇编与机器指令

• 今天才知道解释器是逐行翻译运行，微程序其实与机器指令也存在一种对应关系，具体就是指令的操作码相当于微程序的序号，操作数相当于参数 有点类似一种伪函数调用过程

链接

• 链接是一个相对新奇的东西，在我第一次接触的时候。现在回想一遍，感觉主要思考一个关于重定位的问题。以及最后的加载执行问题就可以了。不过感觉要想真正的完整的认识链接，还是需要在理解了虚拟内存的基础上。